Los conocimientos en Ingeniería Química, disciplina eminentemente práctica, deberán permitir la predicción de lo que sucederá en unas condiciones determinadas o de aquellas condiciones necesarias para que se produzcan determinados fenómenos (separaciones por destilación, precipitación, filtración, etc.).
Como ejemplo del primer caso puede considerarse el saber que si se desea transportar calor mediante agua a 150 ºC y a presión atmosférica, el agua estará en estado vapor. Como ejemplo del segundo caso, puede considerarse el saber que para llevar a ebullición agua, a presión atmosférica, debe alcanzarse una temperatura de 100 ºC.
En Ingeniería Química, las predicciones no siempre son tan fáciles de realizar como pueda parecer en estos ejemplos; a menudo, se debe recurrir a expresiones más o menos complejas para obtener el valor deseado. Estas expresiones interpretan el comportamiento del sistema a estudiar y pueden tener distintos grados de complejidad, incluso para obtener el valor de una misma variable.
Así, la temperatura a la que llega una determinada masa de agua (m) cuando se le suministra cierta cantidad de calor (Q) puede predecirse por aplicación de la siguiente ecuación.
Imagen 1. Ecuación para el cálculo del calor necesario para un incremento de temperatura.
Esta expresión representa la realidad (indica que la aplicación de calor produce una variación en la temperatura del sistema) y permite conocer con una cierta precisión la variación de temperatura provocada. De hecho, la ecuación de la imagen 1 es, simplemente, un modelo que intenta aproximarse a un comportamiento real; en este intento supone que el calor suministrado y el incremento de temperatura originado están relacionados por una constante de proporcionalidad, que es la capacidad calorífica a presión constante por unidad de masa.
La complejidad de los modelos aumenta con su nivel de aproximación a la realidad; por ejemplo, para conocer la temperatura final (Tf) del agua —inicialmente a Ti— con más precisión de la que ofrece la expresión de la ecuación de la imagen 1, se puede utilizar la ecuación siguiente:
Imagen 2. Ecuación para el cálculo del calor necesario para un incremento de temperatura.
Obviamente, el uso de esta ecuación puede llegar a ser mucho más complicado que el de la ecuación anterior, ya que requiere el conocimiento de la función Cp (T) en lugar de un valor promedio único de la misma . En otras palabras: el segundo modelo es más complejo, pero ofrece más precisión; mientras que el primero es más inexacto, pero proporciona el valor deseado en un tiempo menor. Esta comparación ya permite avanzar que el ingeniero químico deberá evaluar, en cada caso concreto, cual es el modelo más conveniente para representar la realidad.
La modelización ingenieril de sistemas reales conduce, frecuentemente, a un conjunto de ecuaciones que relacionan las distintas variables de un sistema. Este conjunto de ecuaciones conforma el modelo de comportamiento del sistema, y debe tenerse en cuenta que es el conjunto de suposiciones sobre el comportamiento de este sistema lo que conduce a las ecuaciones. Así, por ejemplo, el modelo representado por la ecuación de la imagen 1 se basa en suponer que el calor específico es constante en todo el intervalo de temperatura por el que pasa la sustancia a estudiar; lógicamente, al disminuir dicho intervalo se hace más verosímil la suposición.
Es importante tener en cuenta que modelo es todo aquello que intenta representar la realidad; de forma que, no sólo lo es aquel que contiene expresiones matemáticas, sino que los planos, los mapas o las maquetas también son modelos.
Actualmente, se tiende a conseguir modelos muy generales, cuya aplicación a muchos y variados sistemas proporcione buenas estimaciones; estos modelos generales se adaptan a cada sistema concreto por incorporación de sus particularidades.
Es por ello que un vistazo rápido a este módulo puede conducir al error de juzgar extremadamente dificultoso el estudio de los fenómenos de transporte, especialmente al echar un vistazo a las ecuaciones de balance.
Tales ecuaciones — ver imagen 3 — no deben asustar a nadie por su aparente complejidad, ya que son fruto de la elaboración de modelos globales; cuando estas ecuaciones se aplican a un sistema concreto, muchos de sus términos son conocidos o se anulan y las ecuaciones resultantes son menos aparatosas.
Imagen 3. Ecuaciones de balance microscópico de materia (a), energía (b) y cantidad de movimiento (c) en coordenadas cartesianas; densidad y difusividad consideradas constantes.
Según se basen en teorías sobre el comportamiento del sistema o en datos experimentales que describan su comportamiento, se puede distinguir entre modelos teóricos y modelos empíricos.
Como ejemplo de los primeros puede citarse la teoría cinética de los gases; mientras que cualquier curva de solubilidad o de equilibrio líquido-vapor constituye un claro ejemplo de los segundos. La distinción entre ambos tipos de modelo no siempre es clara, ya que un mismo modelo puede englobar teorías y datos empíricos.
Además de los modelos mencionados, existen los modelos analógicos que intentan asimilar un comportamiento real a otro previamente estudiado y modelizado; así, la conducción de calor puede considerarse análoga a la conducción de corriente eléctrica, de forma que un sistema eléctrico puede servir de modelo para un sistema que presente conducción de calor.
Imagen 4. Analogía conducción térmica-eléctrica en serie.
En la práctica, todo modelo debe contrastarse con la realidad para que adquiera validez, y es este contraste el que enriquece al modelo y lo aproxima a la realidad; por ello, cualquier modelo necesita un largo tiempo de estudio y observación antes de ser validado.
Los modelos más utilizados en Ingeniería Química se han desarrollado para pronosticar el comportamiento de los procesos químicos. La predicción de este comportamiento suele realizarse mediante una serie de ecuaciones matemáticas, más o menos complejas, que relacionan las distintas variables del proceso. Gran parte de estas relaciones no son estrictamente ciertas, sino que son estimativas, pero su nivel de aproximación a la realidad puede ser muy elevado. De entre estas relaciones, pueden mencionarse las de equilibrio, las cinéticas o las estimaciones económicas y medioambientales.
Otras relaciones sí son estrictamente ciertas para la mayoría de los procesos; éstas surgen de la aplicación de los principios de conservación. Aunque estas últimas relaciones, denominadas balances, pueden resumirse en una expresión general, su desarrollo es función de la profundidad con la que se desee estudiar el sistema.
Es por ello que resulta conveniente clasificar los modelos según el nivel de descripción de la realidad que intentan conseguir. En este sentido, los modelos se clasifican en macroscópicos, microscópicos y atómico-moleculares. A continuación, se comentan brevemente los tres tipos de modelo.
A. Modelos Macroscópicos
Los modelos macroscópicos son aquellos que sólo aspiran a describir el sistema en cuanto a sus entradas y salidas. Estas entradas o salidas del sistema se entienden como cualquier efecto exterior al sistema que provoque la variación o la constancia del valor dela variable estudiada. La visión de un modelo macroscópico se puede esquematizar en la forma mostrada por la figura de la imagen 5.
Imagen 5. Modelo macroscópico de caja negra.
El sistema se considera como una caja negra, con entradas y salidas, en cuyo interior se produce algún fenómeno cuantificable globalmente: una reacción química con un determinado rendimiento, la separación de un componente dado de una mezcla, la transferencia de cierta cantidad de calor, una caída de presión concreta, etc.
También puede producirse la conjunción de varios fenómenos. Desde este punto de vista, si se puede saber qué ocurre globalmente en el sistema, sólo se requiere conocer la entrada o la salida para evaluar, respectivamente, la salida o la entrada; de igual forma, conocidas la entrada y la salida, se puede cuantificar el comportamiento global del fenómeno que tiene lugar dentro del sistema.
Lógicamente, si el estudio se efectúa a distintos tiempos, los modelos macroscópicos también permiten obtener información sobre la variación con el tiempo de las entradas, de las salidas o de las variables globales del sistema.
Desde la óptica ingenieril, es suficiente un conocimiento macroscópico de los sistemas; sin embargo, para cuantificar algunos fenómenos se necesita averiguar cómo suceden, lo que obliga a entrar en la caja negra y descubrir qué ocurre en su interior, por lo menos hasta un cierto nivel de descripción.
- Éste es el caso del ejemplo siguiente.
El máximo contenido calorífico por unidad de masa de agua se encuentra justo a la salida del calentador, donde la temperatura del agua es mayor y, por lo tanto, en esta sección inicial de la conducción se tiene el máximo potencial de pérdida de calor. El avance del agua a través de la conducción conlleva una disminución de la temperatura del fluido — va perdiendo calor—, lo que aminora el potencial de pérdida de calor. De esta manera, la pérdida de calor y la temperatura del agua van disminuyendo a lo largo de la conducción.
Imagen 6. Capa cilíndrica. Perfil de temperatura.
Las temperaturas de entrada y salida de la conducción original permiten determinar un parámetro, el coeficiente de transferencia de calor, a través del cual se puede conocer la distribución de temperatura y, por lo tanto, la pérdida de calor al doblar la longitud de la conducción. La obtención de este coeficiente de transferencia pasa por una serie de consideraciones que no pueden efectuarse si la conducción se simplifica hasta convertirla en un punto (nivel de descripción macroscópico), sino que requiere conocer los fenómenos presentes en el interior de la conducción; es decir, un nivel de descripción más completo, más interno como el que se expone en la siguiente sección.
B. Modelos Microscópicos
Los modelos microscópicos son aquellos que pretenden describir el interior de un sistema considerando que la materia es continua —como los modelos macroscópicos—; de hecho, no distinguen átomos, moléculas o iones, sino pequeños volúmenes microscópicos contiguos como los mostrados en la figura de la imagen 7.
Imagen 7. Modelo microscópico.
En los modelos macroscópicos se considera el sistema como una caja (punto macroscópico) cuyas propiedades toman el valor promediado de todo lo existente en su interior; en los modelos microscópicos, esa caja se descompone en múltiples puntos físicos cuyas propiedades siguen promediándose, pero ahora en un volumen pequeñísimo. En realidad, se tiene una serie de cajas mucho más pequeñas (puntos microscópicos), el conjunto de las cuales forma el punto macroscópico.
Evidentemente, la posición de cada uno de estos pequeños volúmenes tiene gran relevancia en los modelos microscópicos.
La descripción microscópica de sistemas, objetivo fundamental de este texto, supone el conocimiento de las funciones que siguen las variables dependientes que interesen (temperaturas, concentraciones, velocidades, etc.) con respecto a la posición y al tiempo (variables independientes).
Dado que los modelos microscópicos consideran la materia continua, las propiedades de esta materia también deberán variar de forma continua con la posición (x, y, z) y, por supuesto, con el tiempo (t).
La información proporcionada por los modelos macroscópicos y por los microscópicos presenta una notable diferencia: de los primeros se obtienen los valores de las variables de entrada, salida o globales del sistema, así como su posible variación con el tiempo; mientras que los segundos proporcionan variaciones de las variables, en el interior del sistema, con el tiempo y la posición, es decir, funciones. El conocimiento de lo que ocurre dentro del sistema puede no interesar por sí mismo, pero aquello que sucede en su interior puede afectar a las salidas, y esto sí que interesa conocerlo.
El nivel microscópico de descripción puede permitir cuantificar qué pasaría en un sistema sin necesidad de experimentar en él, y amplía la capacidad de predicción a un mayor número de sistemas respecto de la utilización exclusiva del nivel de descripción macroscópico.
Las propiedades utilizadas en la descripción microscópica de un sistema, matemáticamente, corresponderían a las que tendría el material en una posición —en un punto (x, y, z)— de dicho sistema. Físicamente, no puede ser así; un punto matemático no tiene volumen y, por lo tanto, no puede tener materia, de manera que no se puede hablar de densidad, concentración u otras propiedades de la materia en un punto matemático.
En realidad, como ya se ha comentado, las propiedades evaluadas microscópicamente en un punto (x, y, z) se considera que corresponden al valor medio de tales propiedades para la materia contenida en un volumen alrededor de dicho punto matemático. Este volumen, conocido como elemento de volumen (la figura de la imagen 7 presenta seis de ellos), debe ser suficientemente pequeño para que la variación de las propiedades con la posición, dentro de él, no sea importante; pero, a su vez, debe ser suficientemente grande para que el número de moléculas o átomos sobre los que se promedia sea significativo. De hecho, si se pudiese y quisiese comprobar experimentalmente el valor de una variable, calculado matemáticamente para un punto de un sistema, se debería tomar una muestra de materia tan grande que permitiera la medición de la propiedad y tan pequeña que esta propiedad no variase en la muestra.
El punto más débil de los modelos microscópicos es la hipótesis de materia continua ya que algunos sistemas reales presentan cambios bruscos en los valores de las variables, lo que obligaría a considerar funciones discontinuas para describir microscópicamente la variación de aquellas.
Piénsese, por ejemplo, en la evaporación de un líquido y el repentino descenso de la densidad con la posición al pasar de la fase líquida a la fase gas.
En realidad, la variación de densidad en esta interfase ocurre, gradualmente, en un espesor muy pequeño —de unas pocas moléculas—. Como el nivel de descripción microscópico implica puntos físicos con una cantidad importante de moléculas para que los promedios de las propiedades sean significativos, no es posible describir microscópicamente la variación de la densidad en un espesor de tan pocas moléculas.
Sin embargo, cada una de las dos fases puede modelizarse microscópicamente para obtener funciones continuas de variación de las variables con la posición y el tiempo.
Así pues, los modelos microscópicos se aplicarán a sistemas o subsistemas de una sola fase para evitar las discontinuidades; cuando un sistema presente más de una fase, se modelizará microscópicamente cada una de ellas por separado y, luego, los modelos resultantes se conectarán mediante relaciones de equilibrio o de velocidad.
Los modelos microscópicos proporcionan información general sobre la dependencia de unas variables concretas con el tiempo y la posición —funciones del tipo f(x, y, z, t)—.
Esta información debe adaptarse al sistema concreto a estudiar, lo que requiere conocer algunas de sus condiciones: las que se presentan en su principio y en su final, tanto espacial como temporalmente. Estas condiciones que tienen lugar en los límites del sistema son las denominadas condiciones límite. Los límites espaciales son las superficies físicas que confinan el volumen de todo el sistema al cual se aplica el modelo microscópico; normalmente las interfacies que separan una fase de otra. Los límites temporales son los valores de tiempo inicial y final del periodo considerado para el estudio del sistema. La descripción adecuada de un sistema requiere la inclusión, en el modelo, de estas condiciones que concurren en los límites espaciales, condiciones límite propiamente, y en un límite temporal, condición inicial.
Se puede pensar que las propiedades interesantes, desde el punto de vista ingenieril, son aquellas que se pueden medir; si se pueden medir, es decir, son perceptibles, es porque ejercen alguna influencia sobre el entorno, lo pueden afectar, y, por lo tanto, interesan. Ahora bien, cuando resulta necesario el conocimiento microscópico de un sistema porque las variaciones de las propiedades con la posición en su interior afectan a su salida, entonces debe tenerse muy en cuenta la posibilidad de que estas propiedades estén influidas, a su vez, por otras, analizables sólo a un nivel más interno de descripción que surge de admitir la discontinuidad de la materia. Esta nueva consideración incita al estudio de los sistemas bajo el enfoque atómico-molecular.
C. Modelos Atómico-moleculares
Los modelos atómico-moleculares son aquellos que consideran la materia formada por partículas discretas que interaccionan entre si, que se atraen o repelen dependiendo de la distancia que las separa. Esta característica es la que determina las propiedades de la materia; propiedades que se pueden medir como la densidad, la viscosidad o la temperatura. En estos modelos, el elemento de volumen utilizado por los modelos microscópicos se divide nuevamente hasta el punto de poder distinguir átomos, moléculas o iones (las partículas discretas que forman el sistema a modelizar).
Gracias por dedicar tu tiempo a la lectura de esta entrada; si detectas cualquier error y deseas informarnos, estaremos encantados de recibir tú comunicación.
Referencias bibliográficas
[1] Montserrat Iborra, Javier Tejero. Reactores químicos.
Referencias bibliográficas
[1] Montserrat Iborra, Javier Tejero. Reactores químicos.
[3] Ricard Torres. Fenómenos de transporte.

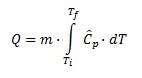





Cap comentari:
Publica un comentari a l'entrada